In pipelined processors, instruction are fetched, decoded, and executed speculatively, and are not permitted to modify system state until instruction commit. For instructions that modify registers, this is often achieved using register renaming. For stores to memory, speculative stores write into a store queue at execution time and only write into cache after the store instructions have committed.
A store queues introduces new problems, however. If a load is data-dependent on an earlier store, the load either has to wait until the store is committed before loading the value from cache, or the store queue must be able to forward the speculative store value to the load (store-to-load forwarding). This requires the processor to know whether a given load depends on an earlier not-yet-committed store, but this is much harder than figuring out register dependencies.
Fig. 1 illustrates the difficulty of learning memory dependencies. Register-carried dependencies (through eax in this code) are easy to figure out because the source and destination registers are specified in the instruction opcode. Memory addresses, on the other hand, are not known until after the address computation is executed. In this example, the lower two bytes of the load depends on the upper two bytes of the store (x86 is little-endian). If we wanted to execute memory instructions out of order (e.g., execute the load before the store), then we would need to know (non-speculative) or predict (speculative) whether a load depends on an earlier store (memory dependence speculation), and then later verify this guess (memory disambiguation).
Store-to-Load Forwarding
When a load depends on a recent earlier store, the data that should be loaded is not yet in the cache, and needs to be forwarded from the store, through the store queue. This can be done by searching the store queue (like a CAM) for a store whose address matches the load, then retrieving the data from the store queue rather than L1 cache if there is a match. However, since x86 allows unaligned memory accesses of varying sizes, there are many combinations that need considering. For example, in Fig. 1, the four-byte load would need to retrieve its lower two bytes from the preceding store, but the upper two bytes from cache. This behaviour is rare, so in x86 implementations so far, forwarding does not happen in this case and the load is delayed until after the store commits.
Searching the store queue CAM is only one way to accomplish this task. There have been references to using some form of set-associative “store forwarding buffer”, and I don’t really know how those work. There are certainly many variations in the implementation details, as there seem to be 6 implementation variations in the nine Intel and AMD microarchitectures I’ve tested. These variations differ in the cases where store-to-load forwarding succeeds or fails, and measuring these delays give some hints as to their implementation.
Memory Dependence Speculation
Early out-of-order processors only did non-speculative out-of-order execution of memory operations. Loads did not execute until all earlier store addresses were known, at which point it is possible to determine with certainty whether the load depends on an earlier store and needs to wait longer. Memory dependence speculation allows predicting if a load depends on earlier stores before the store addresses are known, but runs the risk of incorrectly reordering a load before a store on which it depends. A trivial dependence predictor could predict that loads are never dependent on earlier stores, because in real code most loads are independent of earlier stores, while a better predictor might use past behaviour of the load.
In processors that continue to search a store queue (all of them, as far as I know), speculation does not always need to happen. When a load is executed, it is possible that all earlier store addresses are already known and it is known with certainty whether there is a dependency without needing to speculate. The behaviour for a load that is predicted dependent is not necessarily the same as a load that is known to be dependent.
We can construct microbenchmarks consisting of dependent store and load instructions that differ in whether it forces the processor to speculate on store-load dependencies. Such a microbenchmark can indicate whether a trivial dependence predictor is used, and also whether there is any difference in behaviour for loads that are correctly speculated to be dependent on a store compared to loads that are known to be dependent on a store.
Methodology
Since we’re attempting to measure memory dependence speculation and store-to-load forwarding, we need to construct a microbenchmark that contains loads that are dependent on earlier stores.
// Fast address
repeat {
mov [rdi], rdx
mov edx, [rsi]
mov [rdi], rdx
mov edx, [rsi]
...
}
// Fast data
repeat {
mov [rsi+8], rsp
mov rsi, [rsp+8]
mov [rsi+8], rsp
mov rsi, [rsp+8]
...
}
Fig. 2: Microbenchmark inner loop (Intel syntax, destination operand comes first). Left: fast address, where the store address rdi is available early while the store data rdx is on the critical path. Right: fast data, where the store data rsp is available early and the store address rsi is on the critical path. Note that the load address rsp is also available early.
Fig. 2 shows the inner loop of the two variations of the microbenchmark used. Store instructions have two source operands (store address and store data), and the time at which these operands are available affect whether subsequent load instructions will know earlier store addresses or will need to speculate due to unresolved store addresses.
In the fast address variant (left), the store address uses an unchanging register rdi which allows store addresses to be immediately computed without waiting, with a data dependency through the store data. This dependency is necessary because otherwise the processor would parallelize pairs of instructions and the extra delays due to store-to-load forwarding would not be observable. Because store addresses can be computed early, it is expected that loads would not require memory dependence speculation because all earlier store addresses would already be known, allowing me to measure the latency of store-to-load forwarding without the impact of speculation. The fast address code uses 64-bit stores but 32-bit loads. There is no issue with partial register writes here because x86-64 specifies that the upper 32 bits of a 64-bit register are always zeroed in a 32-bit operation.
In the fast data variant (right), store data and load data values use the unchanging register rsp, but there is a data dependence from the load to the store address. This data dependency makes it slow to resolve store addresses, so load execution would generally occur while there are still many earlier stores with unresolved addresses, which exercises the memory dependence speculation behaviour. This code is constructed so that loads always depend on the previous store, so it should be easy to predict. In the ideal case, the predictor should always realize that loads depend on an earlier store and this case should not cost more than the fast address case on highly-predictable code. Surprisingly, I find that this isn’t the case on many of the microarchitectures tested.
Another feature of the fast address code in Fig. 2 is that it uses two different registers for the load and store addresses. This is to allow testing the latency for the many different cases of overlap (load not dependent on store, partial overlap, etc.) and also to observe the interaction with the absolute value of the addresses, for penalties involved with crossing cache line (or other) boundaries.
Hardware
Nine microarchitectures were tested:
| Yorkfield | Core 2 Quad Q9550 (45 nm) |
|---|---|
| Lynnfield | Core i7-860 |
| Sandy Bridge | Core i5-2500K |
| Ivy Bridge | Core i5-3570K |
| Haswell | Pentium G3420 |
| Agena | Phenom 9550 |
| Thuban | Phenom II 1090T |
| Bulldozer | FX-8120 |
| Piledriver | FX-8320 |
To my knowledge, Agena and Thuban do not do speculative loads, while the rest of the processors do.
Results
Memory dependence speculation: Fast address vs. fast data
Here are results for running the above microbenchmarks with load and store addresses equal, and both addresses at least 8-byte aligned. For reference, the L1 cache hit latencies are included. All latencies are in units of clock cycles.
| Processor | L1 hit time | Fast address | Fast data | Fast data, no address reuse |
|---|---|---|---|---|
| Yorkfield | 3 | 5.04 | 4.01 | 4.01 |
| Lynnfield | 4 | 5.14 | 6.02 | 5.66 |
| Sandy Bridge | 4 | 5.32 | 9.80 | 7.65 |
| Ivy Bridge | 4 | 5.00 | 13.01 | 13.01 |
| Haswell | 4 | 5.07 | 12.21 | 11.58 |
| Agena | 3 | ~4.5 | 8.02 | 8.02 |
| Thuban | 4 | ~4.5 | 8.01 | 8.01 |
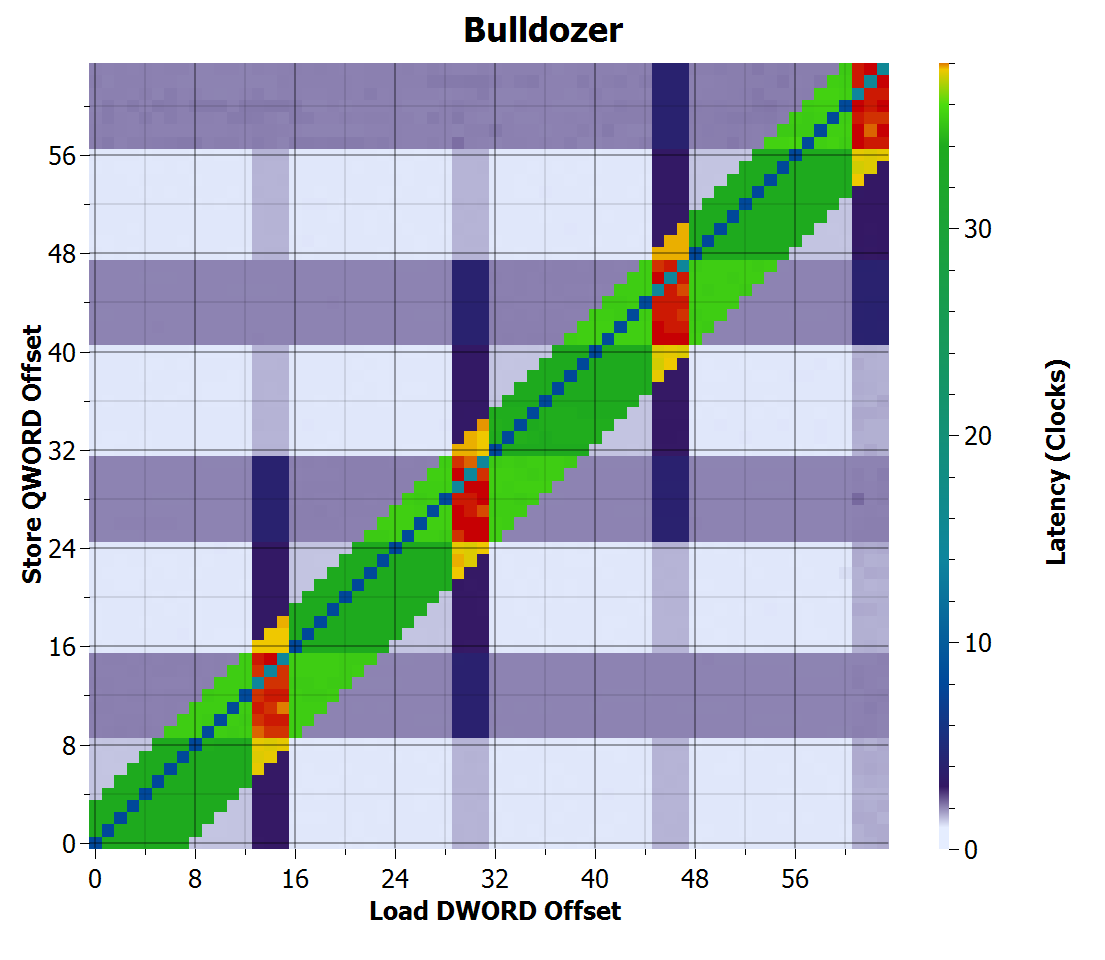
| Bulldozer | 4 | 8.02 | 35.2* | 37.6* |
| Piledriver | 4 | 8.02 | 39.8* | 40.0* |
* The fast data numbers for Bulldozer and Piledriver increase somewhat with the amount of loop unrolling, and thus probably isn’t a true latency number.
The fast address latencies are what would normally be considered the store-to-load forwarding latency. It’s not surprising, but still interesting to note that they are consistently greater than the L1 cache latency.
The fast data latencies indicate what happens when the processor is forced to speculate on whether a load depends on an earlier store. Since the access pattern I used is easy to predict, I would expect fast data latencies to be similar to fast address. This is generally true for Intel Yorkfield and Lynnfield, but have gotten significantly worse in newer Intel microarchitectures. The Sandy Bridge, Ivy Bridge, and Haswell latencies are lower than the delay for impossible-to-forward cases and seem lower than a full pipeline flush, so these do not appear to be a failure of the dependence predictor. It probably hints at some simplification of the hardware that handles the predicted-dependent case because it doesn’t happen often.
The AMD Agena and Thuban microarchitectures are not supposed to speculate, yet the fast data latencies are higher than fast address. This may indicate that store addresses take several cycles to be resolved and inserted into the store queue CAM before they’re available for a load to use for dependence checking.
But what happened to Bulldozer and Piledriver? The fast data latencies are very high (30+ cycles), enough to be full pipeline flushes. The measured latencies also increase somewhat with increased loop unrolling (currently unrolled 64 load+stores), which again suggest that these are true pipeline flushes whose cost depends somewhat on how many instructions need to be flushed out. If these are true pipeline flushes, the likely conclusion is that Bulldozer and Piledriver do not use a dynamic dependence predictor and simply predict all loads as independent on earlier stores, thus mispredicting every time for this microbenchmark.
The fact that the fast data latencies have increased in Intel processors raises the question of whether the hardware simplifications are with the hardware that wakes up load instructions after they have been predicted to be dependent and made to wait. It is too expensive for every outstanding load to check every earlier store every cycle, but there are still many design options:
- Stall all subsequent loads while waiting for earlier stores to complete?
- Put the load instruction in a queue, and wake up the load when it becomes the oldest instruction?
- Or perhaps wake up the load when a store with an address that matches the load executes?
I don’t draw any firm conclusions on this aspect of the hardware design, but I did one additional experiment to see whether the last option may be a factor. In the fast data microbenchmark in Fig. 1, every load and store occurs to the same address, which has the potential to confuse any address-based wakeup mechanism by having a store wake up the wrong instance of the load (since all of the loads have the same address). The “fast data, no address reuse” variant (code not shown) gives every store-load pair a different address for each instance in the unrolled loop, for a total of 64 unique addresses (spaced 8 bytes apart). A difference in the “fast data, no address reuse” latency compared to “fast data, all addresses the same” would suggest that the load and store addresses are considered during load wakeup. This seems to be the case with Lynnfield, Sandy Bridge, and Haswell, but not the others, and using distinct addresses seems to be slightly faster in all cases where it does makes a difference. However, Haswell and Lynnfield only have a small 5-6% difference, so I am not entirely confident that all other causes have been ruled out.
Store-to-Load Forwarding Latency (Fast Address)
The previous section’s fast address results showed the store-to-load forwarding latency for the ideal case of having load and store addresses equal and addresses aligned. How the processor handles non-ideal cases can reveal details about the mechanism used to do forwarding. Non-ideal cases include cases where a larger store forwards to a smaller load where the addresses are not equal (e.g., load contained inside store), and also cases where the values of the addresses interact with cache line boundaries (64 bytes in all nine processors) and possibly other set-associative structures (store forwarding buffers?).
The following charts plot latency for doing a 8-byte store followed by a 4-byte load, for all 64 values of the low 6 bits of each store and load addresses, for a total of 4,096 data points. Because cache lines are 64 bytes long, I assume behaviour is the same when addresses are incremented by multiples of 64.
More precisely, this experiment performs the following two operations, for all 4,096 combinations of load and store offsets:
- store register to address { array[63:6], store_offset[5:0] }
- load from { array[63:6], load_offset[5:0] } into the same register
I also experimented with two-byte and one-byte loads (with 8-byte stores). Some chips take an extra 1-1.5 cycles to load into a small register, but the results were generally the same as for 4-byte loads, except for Yorkfield, which can forward the second four-byte DWORD of an 8-byte aligned 8-byte store, but can’t do something similar for any of the smaller sizes.
The same chart, animated. Bigger: [Ogg Theora][H.264]
| Colour | Latency | Comment |
|---|---|---|
| 1.0 | Load independent from store gets a throughput of one per clock (not a true latency measurement) | |
| 2.9 | Some form of address comparison occurs at an eight-byte granularity | |
| 5.0 | Successful store-to-load forwarding | |
| 10.7 | Penalty for a cross-cache line store when load is independent. | |
| 12.0 | Unable to forward because only part of the load forwards from a store. | |
| 13.1 | Penalty for a cross-cache line load when load is independent | |
| 15.0 | Penalty for a cross-cache line store when a load depends on it. | |
| 23.1 | Penalty for a cross-cache line store when a cross-cache line load depends on it. |
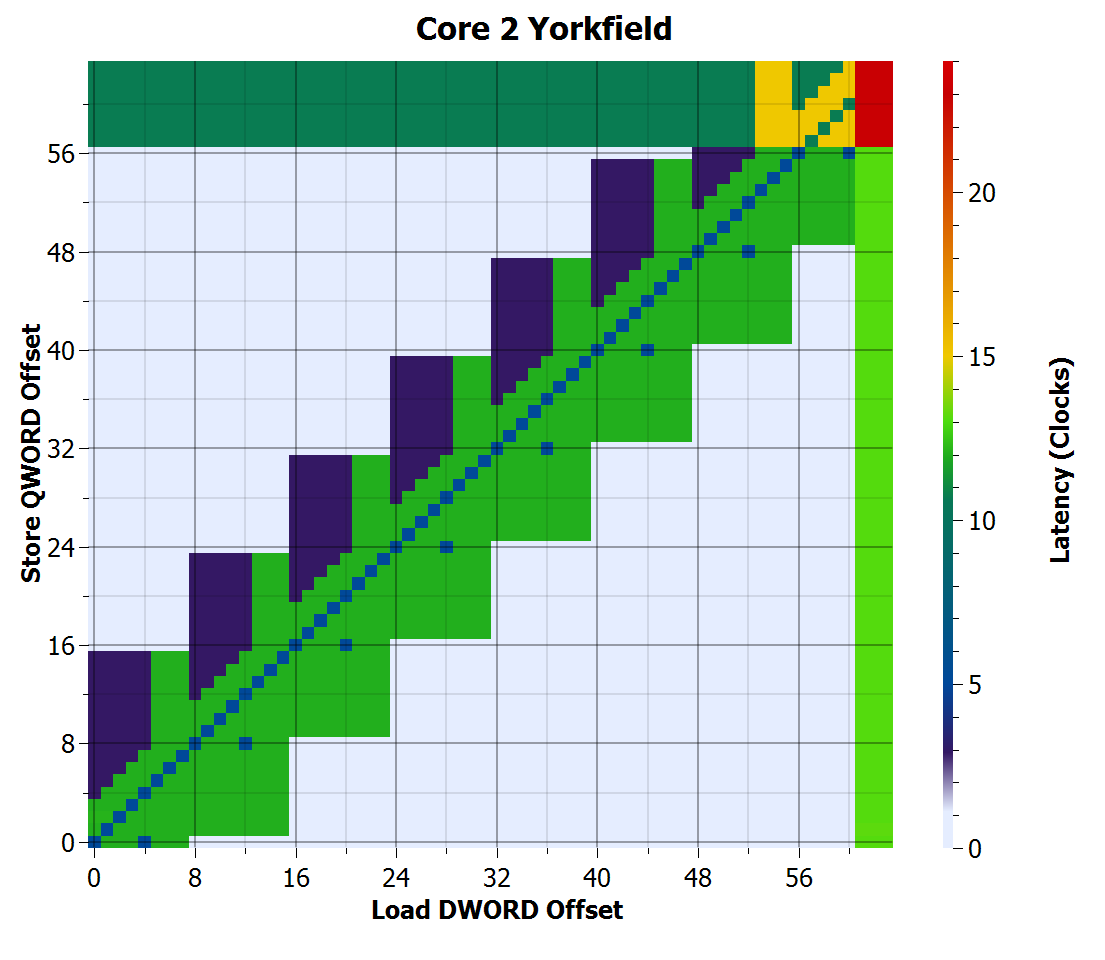
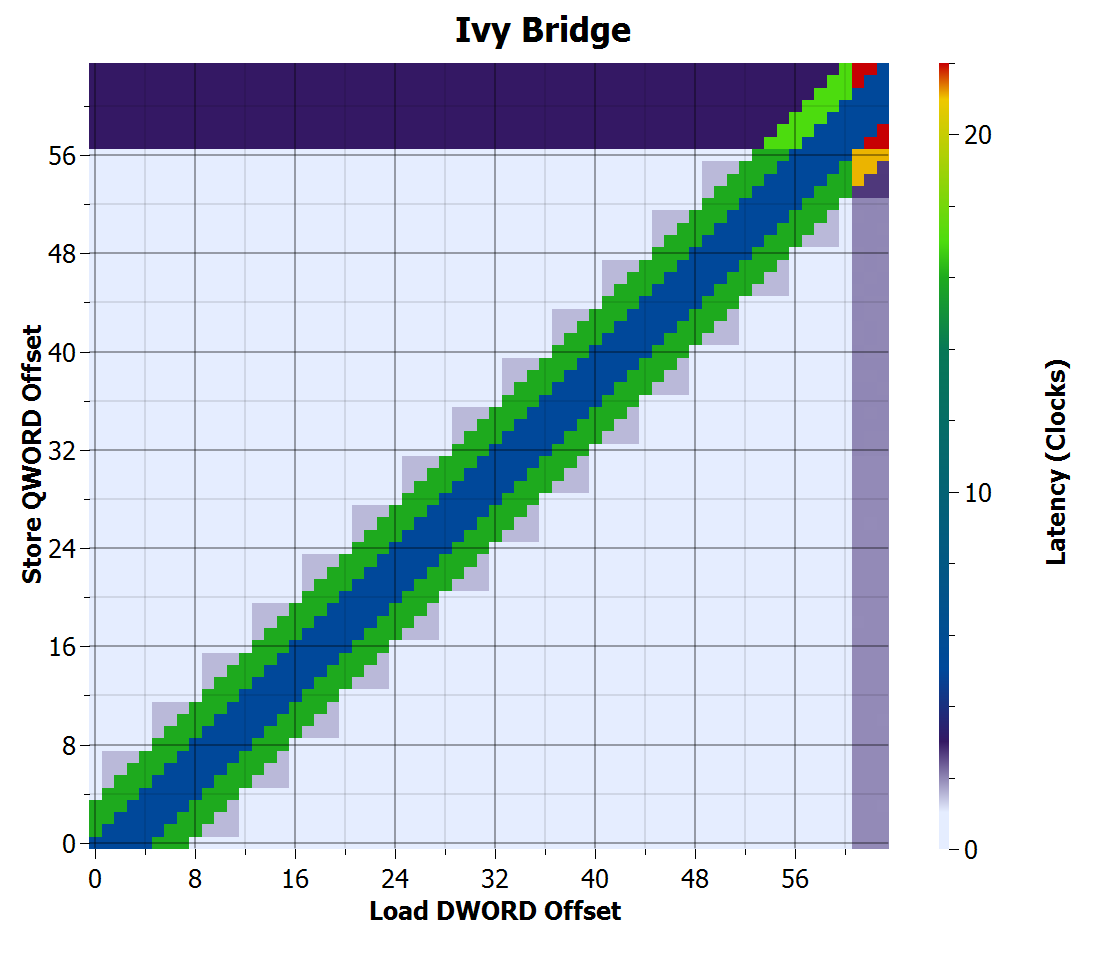
Here are the results for Yorkfield. The x and y axes are the load and store offsets, respectively, and range from 0 to 63. The latency is indicated by colour. Colours are not chosen to be particularly linear, but were chosen to make the latency variations visible. On the right is a 3D chart where the vertical axis represents the latency, to illustrate how the colours correspond to latency values.
The points along the main diagonal where store offset equals load offset are the easy to forward cases. When the store offset is sufficiently different from the load offset, the load becomes independent of the store and the dependency chain is broken, allowing the processor to execute at a rate of one load and store per clock cycle.
There are several interesting features in the above chart.
The increased latency at store offsets greater than 56 and load offsets greater than 60 where the load is independent of the store indicate the penalty for the store or load crossing 64-byte cache line boundaries. The penalty is particularly bad when both store and load span cache line boundaries.
Along the main diagonal, the latency is 5 cycles, indicating a successful store-to-load forwarding. However, this also shows that Yorkfield cannot forward a larger load to a smaller store if their addresses are not equal, even if the load is entirely contained in the store, except for 8-byte aligned stores forwarding the upper 4 bytes to a load (the diagonal row of dots to the right of the main diagonal).
It can also be seen that there are many cases where the load does not overlap the store where the processor is unable to forward, creating big rectangles of green near the diagonal. This indicates that dependence detection occurs in 8-byte blocks, and is somewhat more pessimistic than strictly necessary. I cannot explain the purple regions that are symmetric to the green, but with much lower penalty.
It is also interesting to notice that store-to-load forwarding can occur even if the store crosses a cache line boundary, but cannot when the load crosses a cache line boundary, even if the load address matches the store address. The 5-cycle latency along the main diagonal does not continue into the small red region in the upper-right corner.
Following are charts for the other 8 microarchitectures. No 3D videos, sorry 🙂
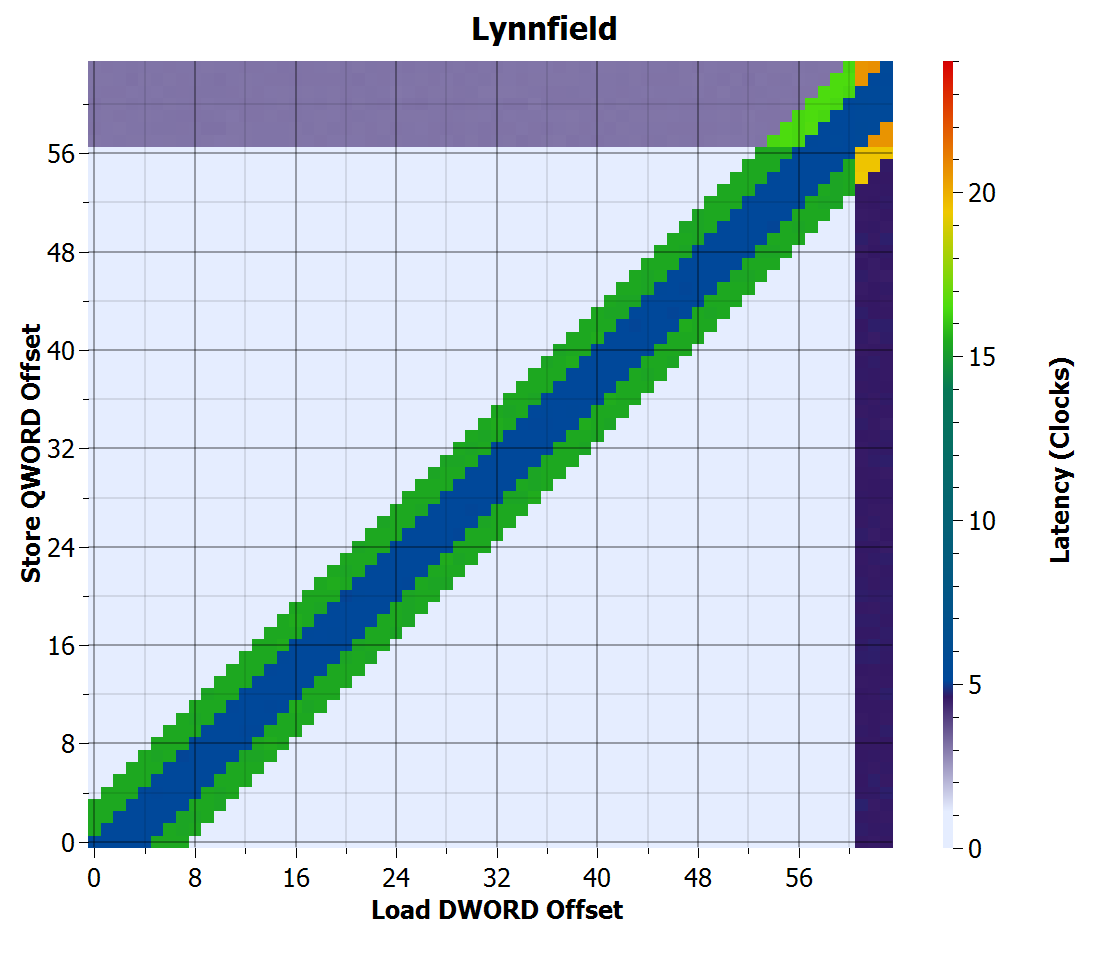
Lynnfield store-to-load forwarding improved significantly. Forwarding only fails for partial overlap of a load with a store, and succeeds even in cases where both the load and store cross cache lines. The penalties for stores and loads that cross cache lines are reduced from Yorkfield (3 cycles for store, 4.6 for load), but still significant.
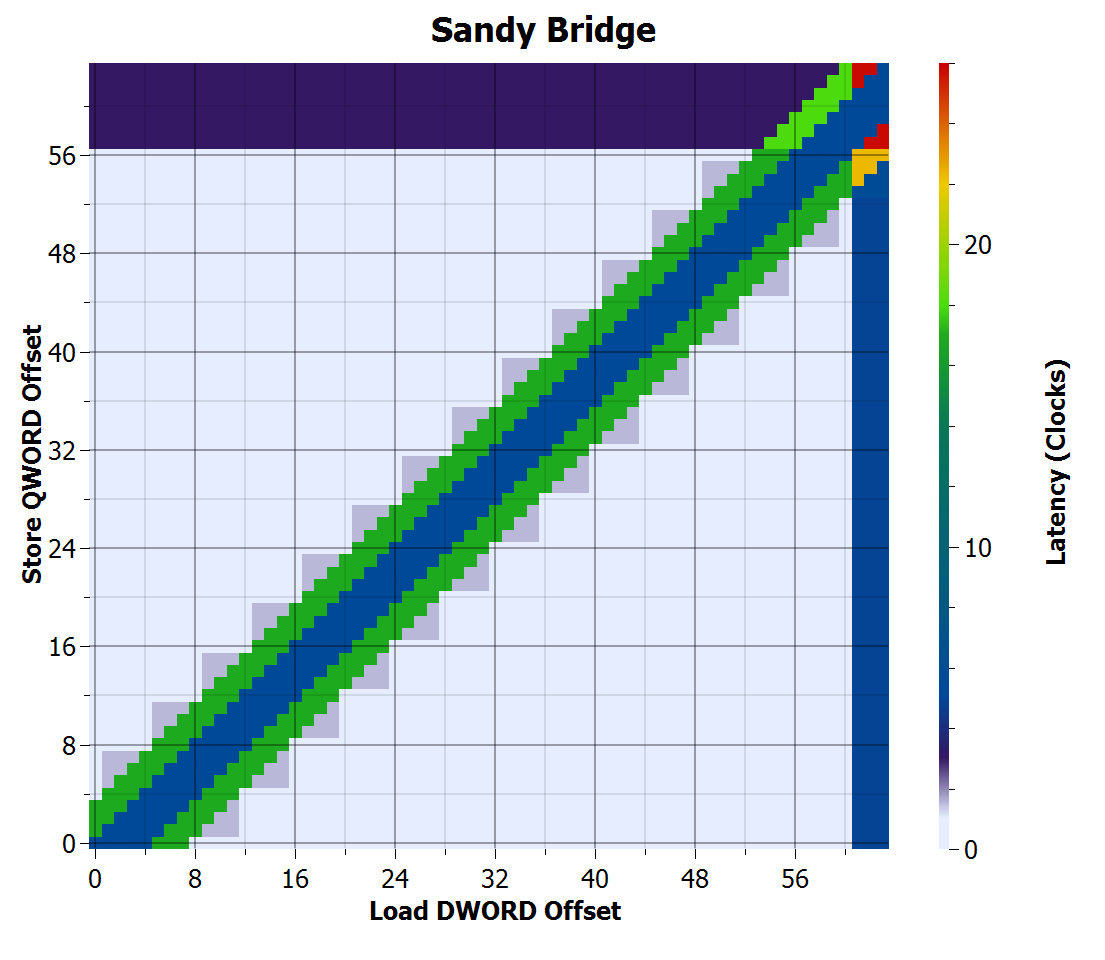
Sandy Bridge behaves similarly to Lynnfield, but cross cache line penalties are slightly higher (3 cycles for store, 4.9 for load). What’s interesting is that there is now a small latency increase (1.5 cycles) in a pattern that suggests something happens at a four-byte granularity. I don’t know what it is, but it does suggest that Sandy Bridge’s hardware differs from Lynnfield, while offering almost the same performance.
Ivy Bridge looks the same as Sandy Bridge, except loads that cross cache lines are faster (2 cycles).
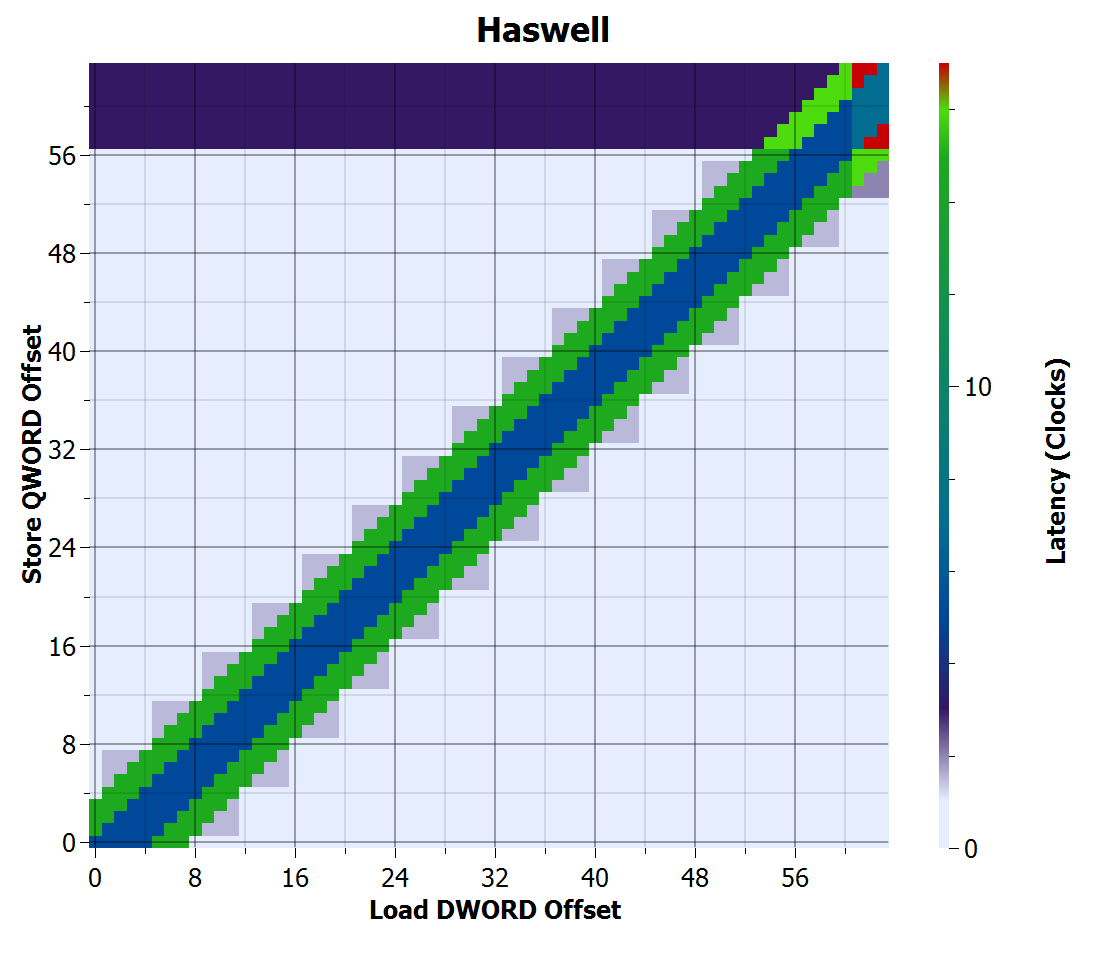
Haswell also looks the same as Sandy Bridge, except the penalty for cross-cache line loads appears to be gone. I speculate there is still a penalty, but because Haswell now has one more store execution unit compared to earlier microarchitectures (2 load-or-store and 1 store per cycle), it has enough throughput to hide the small penalty in this case.
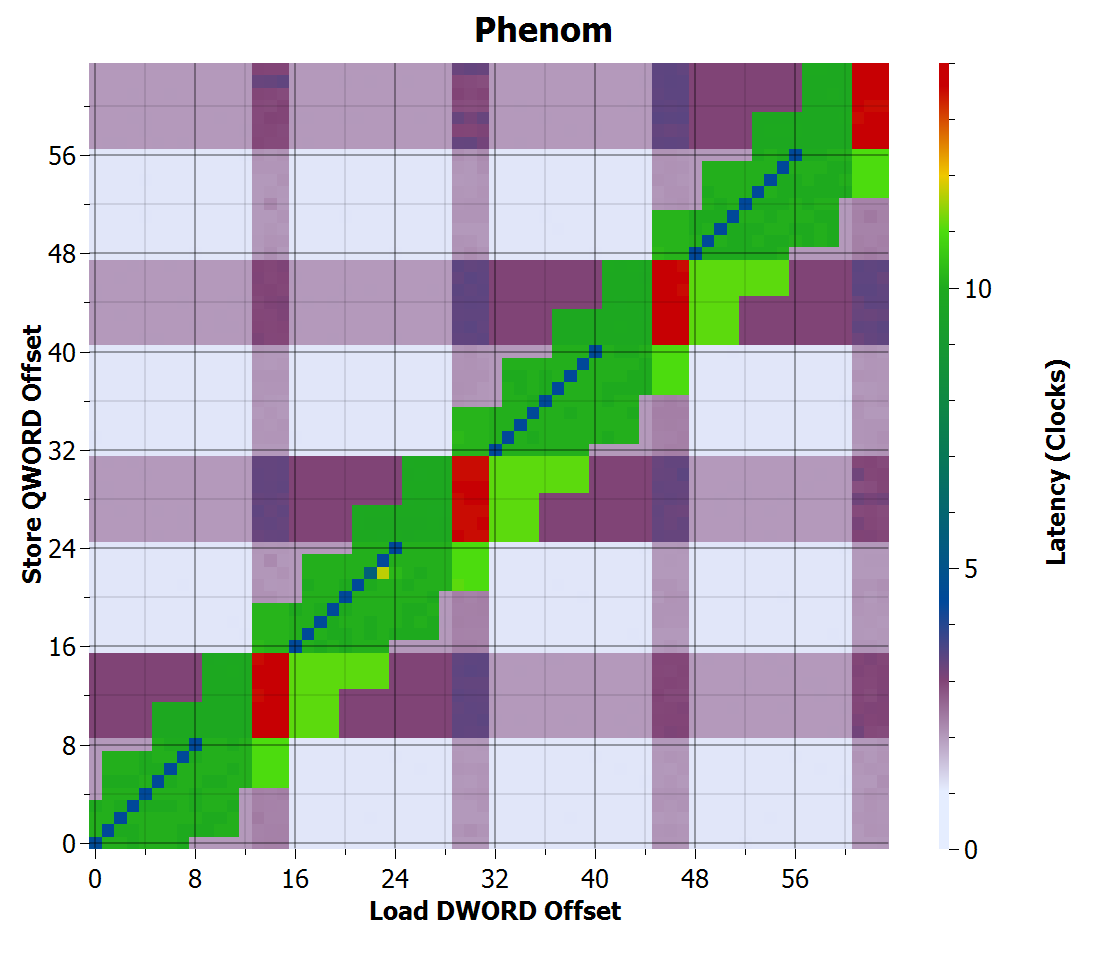
AMD Agena’s behaviour has some resemblance to Yorkfield, but address comparisons seem to use 4-byte granularity instead of 8-byte. However, it fails to forward whenever the store crosses a 16-byte boundary, and is particularly bad when both the load and store cross 16-byte boundaries. The cache line size is 64 bytes, so I don’t know why there is a restriction with 16 byte boundaries.
The low-latency purple grid across the background (2 and 3 cycles) suggests that there is a penalty for crossing 16-byte boundaries even when the accesses are independent.
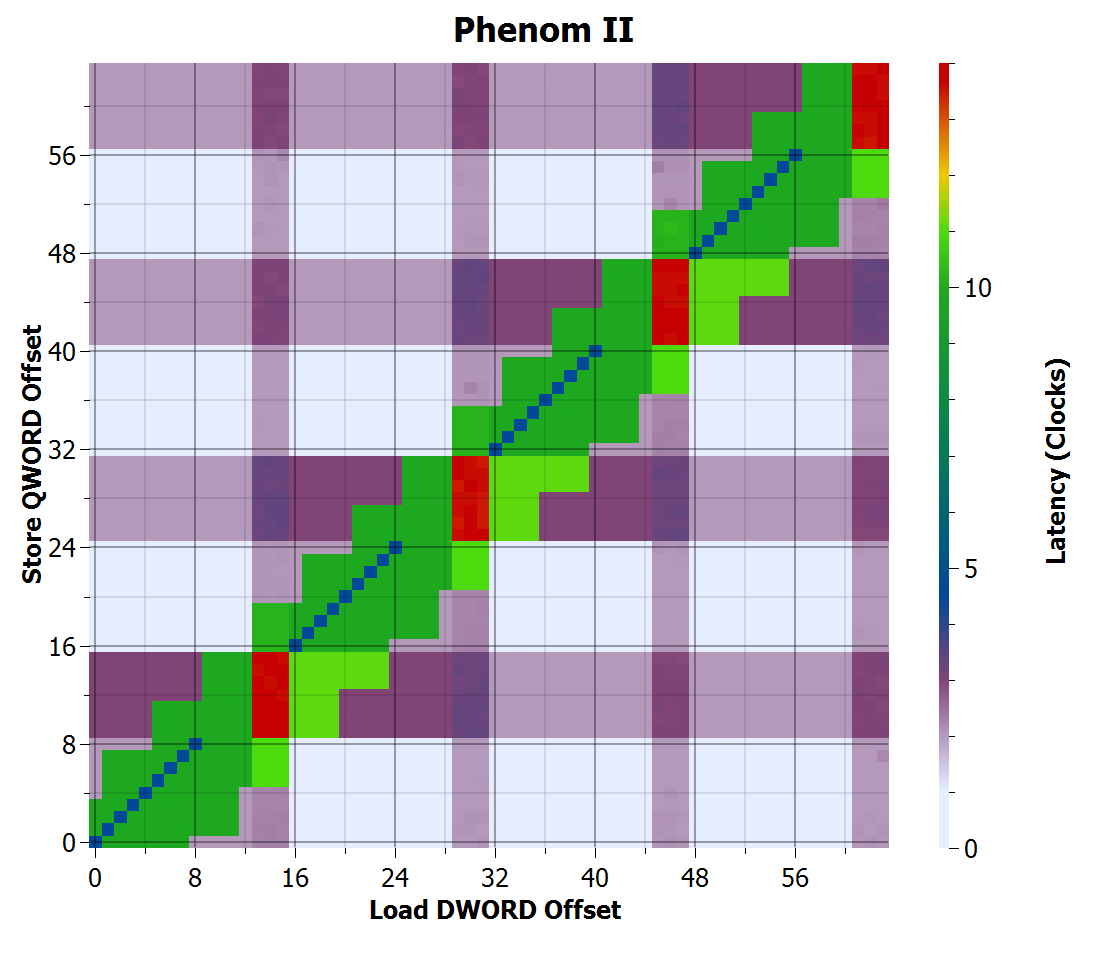
Thuban looks identical to Agena.
Bulldozer appears to be a significant redesign, where forwarding fails only when a load overlaps with a store, and it is now capable of forwarding all cases where the load and store address are equal. Interestingly, there is still a penalty when crossing 16-byte boundaries, rather than at 64-byte cache line boundaries.
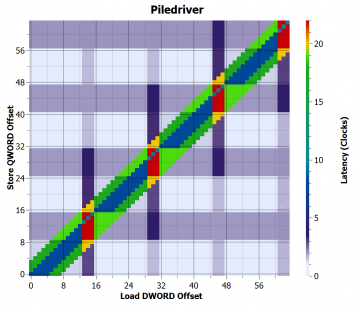
Piledriver improves on Bulldozer, and now forwards all cases where loads are completely contained within a store, with one exception: When a load crosses a 16-byte boundary, forwarding only occurs when load and store addresses are equal, similar to the limitation in Bulldozer. The penalties for crossing 16-byte boundaries remain.
Conclusions
I described two variations of a microbenchmark that can measure some aspects of store-to-load forwarding and memory dependence speculation in processors. The same instruction sequence can be constructed to either compute store addresses early to avoid needing to speculate on dependencies, or to compute store addresses late to force the processor to speculate. I then used these microbenchmarks to show that AMD’s Bulldozer and Piledriver processors likely do not use a dynamic memory dependence predictor, and used the fast address microbenchmark with varying load and store addresses to generate interesting 2D charts that can reveal some details about how the memory execution hardware might be designed.
Intel’s modern implementations of store-to-load forwarding succeeds in almost all cases where it is practical to forward. The only case where forwarding fails (load partially needs to forward) occurs rarely in practice, so it is probably not worth implementing hardware to improve this. The high penalty for a correctly-predicted dependent load is a bit of a concern though, as it is now more than 3× worse than for the older Yorkfield.
Despite 64-byte cache lines, AMD chips seem to unnecessarily penalize accesses that cross 16-byte boundaries. Forwarding has improved with each microarchitecture, but is still slightly behind Intel on handling corner cases, although the remaining corner cases only occur rarely. However, the apparent lack of a memory dependence predictor on Bulldozer and Piledriver and the resulting ~30-50 cycle penalty (presumed pipeline flush) for a misprediction may cause a significant loss in performance.
I haven’t spent as much time as I would have liked in trying to interpret the various patterns in these plots. I think it is possible to infer more details about the underlying hardware by examining the plots in more detail.
Outstanding Questions
- When a load is predicted or known to be dependent on a store, does it hold up the load pipeline, or is there a separate buffer/scheduler where the load will wait?
- Some of these behaviours ought to be different when crossing 4-KB page boundaries than when merely crossing 64-byte cache line boundaries.
Code
Caution: Not well documented.
Cite
- H. Wong, Store-to-Load Forwarding and Memory Disambiguation in x86 Processors, Jan., 2014. [Online]. Available: http://blog.stuffedcow.net/2014/01/x86-memory-disambiguation/
[Bibtex]@misc{x86stlf, author={Henry Wong}, title={Store-to-Load Forwarding and Memory Disambiguation in {x86} Processors}, month={jan}, year=2014, url={http://blog.stuffedcow.net/2014/01/x86-memory-disambiguation/} }
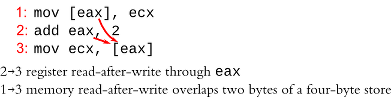
The dynamic dependence predictor exists in Piledriver.
But there is 9 load+stores unrolled, the predictor vanishes.
I ran your “fast data” microbenchmark on my FX-8350, found that it takes only 10 clocks per store-lood-loop.
Not over 30+ clocks as you got.
In addition, I tried to unloop the benchmark, as you mentioned that the amount of loop unrolling affects.
Then the latency increased to 23 clocks.
(Don’t warry it can’t reach 30+ clocks, because I added a loop counter in your bench.)
I seeked latency for each amount of loop unrolling, found the gap between 8 unrolls and 9 unrolls.
When there is unrolled 8 load+stores, predictor in Piledriver works well with 10 clocks latency.
But there is 9 load+stores unrolled, the predictor vanishes.
I suppose the predictor counts only last 8 speculations.
In this assumption, the predictor forgets every the last 9th speculative load, which is the next load to predict in 9 load+stores loop.
So it misses to predict every next load.
That’s a very interesting observation! I hadn’t thought of trying so few unrolls. Yes, I was able to reproduce this on my FX-8320 and FX-8120.
I get 10 cycles for 1-8 unrolls, 22 cycles for 9 unrolls growing ~linearly to 39.4 cycles at 35 unrolls, then nearly flat until at least 64 unrolls (39.8 cycles).
(Similar for Bulldozer FX-8120, but 14 cycles for 1-8 unrolls, ~20 cycles at 9 unrolls)
I think you’re right about this hinting that something in their predictor has size 8. It doesn’t quite explain why latency grows slowly from 9 to 35 unrolls, rather than jumping straight to ~40 cycles though. (Maybe a non-LRU replacement policy?)
Thanks!
Also, I found that running this bench by 8 parallel process (2 threads per bulldozer-module) halve the predctor.
when I run 8 process, the gap appear between 4 unrolls and 5 unrolls.
As I posted to another blog
http://www.agner.org/optimize/blog/read.php?i=187
these two core in a Bulldozer module seem to share not only their decoder but also their load-store unit.
Hmm… Getting almost exactly half the throughput with two threads seems like something is shared. But I don’t think sharing the load/store unit and L1 cache makes much sense. If the load/store unit were shared, the L1 data caches wouldn’t be placed far apart, as seen in the die photo: http://i.imgur.com/b33tNAp.jpg
The memory dependence predictor being shared seems plausible if it’s located in decode (and searched by EIP?)
Hi Henry – these are very interesting results, and well presented – the 2D charts make it easy to pick out the interesting corner cases.
Is the code for the benchmark available? A-11 seems to have run it, but the link is eluding me. I’m interested also in the code for the other benchmarks you wrote about (cache behavior and ROB capacity).
Thanks 🙂
No, I haven’t posted the code anywhere, but I could do so, on the understanding that the code is messy 😛
I think A-11 wrote his own version. He seems to have been looking at L1 bandwidth, which I haven’t tried.
Hello,
this is a very impressive study.
As an additional application for your benchmarking technique, could you look at this question about keeping secrets from being reflected in execution time and see if it inspires you? It may need the benchmark to be slightly adjusted so as to measure the correlation between the value being written over being the same as the previous value and the time of a subsequent read, but if you still have some or all of the hardware and software in place, it would be very interesting (*I* would find it very interesting anyway).
http://stackoverflow.com/questions/29149058/does-memory-dependence-speculation-prevent-bn-consttime-swap-from-being-constant
Hi, thanks!
The question you asked there is rather interesting. I didn’t think the case of overwriting a memory location with the same value had a practical use. I think the answer is that in current processors, the value of the store is irrelevant, only the address is important.
Out here in academia, I’ve heard of two approaches to doing memory disambiguation: Address-based, or value-based. As far as I know, current processors all do address-based disambiguation.
I think the current microbenchmark has some evidence that the value isn’t relevant. Many of the cases involve repeatedly storing the same value into the same location (particularly those with offset = 0). These were not abnormally fast.
Address-based schemes uses a store queue and a load queue to track outstanding memory operations. Loads check the store queue to for an address match (Should this load do store-to-load forwarding instead of reading from cache?), while stores check the load queue (Did this store clobber the location of a later load I allowed to execute early?). These checks are based entirely on addresses (where a store and load collided). One advantage of this scheme is that it’s a fairly straightforward extension on top of store-to-load forwarding, since the store queue search is also used there.
Value-based schemes get rid of the associative search (i.e., faster, lower power, etc.), but requires a better predictor to do store-to-load forwarding (Now you have to guess whether and where to forward, rather than searching the SQ). These schemes check for ordering violations (and incorrect forwarding) by re-executing loads at commit time and checking whether their values are correct. In these schemes, if you have a conflicting store (or made some other mistake) that still resulted in the correct result value, it would not be detected as an ordering violation.
Could future processors move to value-based schemes? I suspect they might. They were proposed in the mid-2000s(?) to reduce the complexity of the memory execution hardware.