Caches are used to store a subset of a larger memory space in a smaller, faster memory, with the hope that future memory accesses will find their data in the cache rather than needing to access slower memory. A cache replacement policy decides which cache lines should be replaced when a new cache line needs to be stored. Ideally, data that will be accessed in the near future should be preserved, but real systems cannot know the future. Traditionally, caches have used (approximations of) the least-recently used (LRU) replacement policy, where the next cache line to be evicted is the one that has been least recently used.
Assuming data that has been recently accessed will likely be accessed again soon usually works well. However, an access pattern that repeatedly cycles through a working set larger than the cache results in 100% cache miss: The most recently used cache line won’t be reused for a long time. Adaptive Insertion Policies for High Performance Caching (ISCA 2007) and a follow-on paper High performance cache replacement using re-reference interval prediction (RRIP) (ISCA 2010) describe similar cache replacement policies aimed at improving this problem. The L3 cache on Intel’s Ivy Bridge appears to use an adaptive policy resembling these, and is no longer pseudo-LRU.
Measuring Cache Sizes
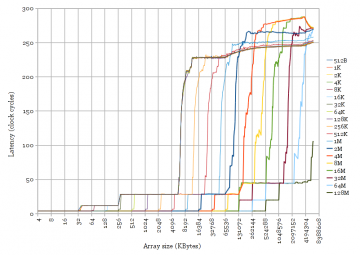
The behaviour of LRU replacement policies with cyclic access patterns is useful for measuring cache sizes and latencies. The access pattern used to generate Figure 1 is a random cyclic permutation, where each cache line (64 bytes) in an array is accessed exactly once in a random order before the sequence repeats. Each access is data-dependent so this measures the full access latency (not bandwidth) of the cache. Using a cyclic pattern results in sharp changes in latency between cache levels.
Figure 1 clearly shows two levels of cache for the Yorkfield Core 2 (32 KB and 6 MB) and three levels for the other three. All of these transitions are fairly sharp, except for the L3-to-memory transition for Ivy Bridge (“3rd Generation Core i5”). There is new behaviour in Ivy Bridge’s L3 cache compared to the very similar Sandy Bridge. Curiosity strikes again.
Ivy Bridge vs. Sandy Bridge
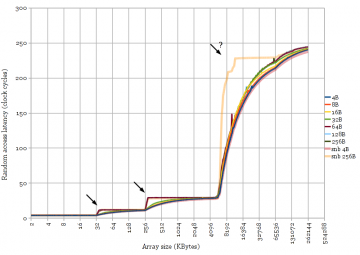
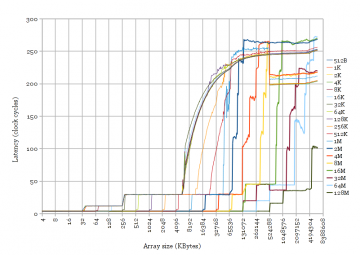
Figure 2: Varying the stride of the random cyclic permutation access pattern for Ivy Bridge and Sandy Bridge. Sharp corners appear when stride >= cache line size, except for Ivy Bridge L3. [png][pdf]
Figure 2 shows a comparison of Sandy Bridge and Ivy Bridge, for varying stride. The stride parameter affects which bytes in the array are accessed by the random cyclic permutation. For example, a stride of 64 bytes will only access pointers spaced 64 bytes apart, accessing only the first 4 bytes of each cache line, and accessing each cache line exactly once in the cyclic sequence. A stride less than the cache line size results in accessing each cache line more than once in the random sequence, leading to some cache hits and transitions between cache levels that are not sharp. Figure 2 shows that Sandy Bridge and Ivy Bridge have the same behaviour except for strides at least as big as the cache line size for Ivy Bridge’s L3.
There are several hypotheses that can explain an improvement in L3 cache miss rates. Only a changed cache replacement policy agrees with observations:
- Prefetching: An improved prefetcher capable of prefetching near-random accesses would benefit accesses of any stride. Figure 2 shows no improvement over Sandy Bridge for strides smaller than a cache line.
- Changed hash function: This would show a curve with a strange shape, as some parts of the array see a smaller cache size while some other parts see a bigger size. This is not observed.
- Changed replacement policy: Should show apparent cache size unchanged, but transitions between cache levels may not show the sharp transition seen with LRU policies. This agrees with observations.
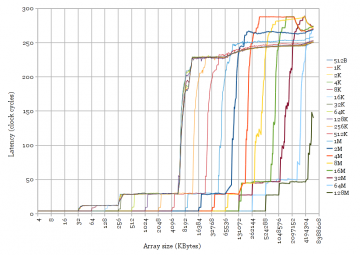
Figure 3 shows two plots similar to Figure 2 for larger stride values (512 bytes to 128 MB). The curved shape of the plots for Ivy Bridge is clearly visible for many stride values.
Adaptive replacement policy?
An interesting paper from UT Austin and Intel from ISCA 2007 (Adaptive Insertion Policies for High Performance Caching) discussed improvements to the LRU replacement policy for cyclic access patterns that don’t fit in the cache. The adaptive policy tries to learn whether the access pattern reuses the cache lines before eviction and chooses an appropriate replacement policy (LRU vs. Bimodal Insertion Policy, BIP). BIP places new cache lines most of the time in the LRU position, the opposite behaviour of LRU.
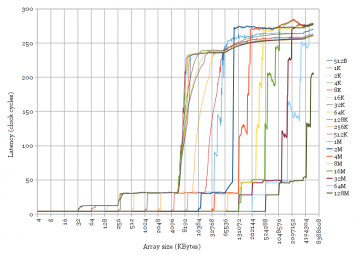
Testing for an adaptive policy can be done by attempting to defeat it. The idea is to trick the cache into thinking that cached data is reused, by modifying the access pattern to reuse each cache line before eviction. Instead of a single pointer chase by repeating p = *(void**)p, the inner loop was changed to do two pointer chases p = *(void**)p; q = *(void**)q;, with one pointer lagging behind the other by some number of iterations, designed to touch each line fetched into the L3 cache exactly twice before eviction. Figure 4 plots the same parameters as Figure 3 but with the dual pointer chase access pattern. The Ivy Bridge plots closely resemble Sandy Bridge, showing that the replacement policy is adaptive, and has been mostly defeated.
Since Ivy Bridge uses an adaptive replacement policy, it is likely that the replacement policy is closely related to the one proposed in the paper. Before we probe for more detail, we need to look a little more closely at the L3 cache.
Ivy Bridge L3 Cache
The L3 cache (also known as LLC, last level cache) is organized the same way for both Sandy Bridge and Ivy Bridge. The cache line size is 64 bytes. The cache is organized as four slices on a ring bus. Each slice is either 2048 sets * 16-way (2 MB for Core i7) or 2048 sets * 12-way (1.5 MB for Core i5). Physical addresses are hashed and statically mapped to each slice. (See http://www.realworldtech.com/sandy-bridge/8/) Thus, the way size within each slice is 128 KB, and a stride of 128 KB should access the same set of all four slices using traditional cache hash functions.
Figure 3 reveals some information about the hash function used. Here are two observations:
- Do bits [16:0] (128KB) of the physical address map directly to sets? I think so. If not, the transition at 6 MB would be spread out somewhat, with latency increasing over several steps, with the increase starting below 6 MB.
- Is the cache slice chosen by exactly bits [18:17] of the physical address? No. Higher-order address bits are also used to select the cache slice. In Figure 3, the apparent cache size with 256 KB stride has doubled to 12 MB. It continues to double at 512, 1024, and 2048 KB strides. This behaviour resembles a 48-way cache. This can happen if the hash function equally distributes 256 through 2048 KB strides over all four slices. Thus, some physical address bits higher than bit 20 are used to select the slice, not just bits [20:17]. Paging with 2 MB pages limits my ability to test physical address strides greater than 2 MB.
Choosing a Policy using Set Dueling
Adaptive cache replacement policies choose between two policies depending on which one is appropriate at the moment. Set dueling proposes to dedicate a small portion of the cache sets to each policy to detect which policy is performing better (dedicated sets), and the remainder of the cache as follower sets that follow the better policy. A single saturating counter compares the number of cache misses occurring in the two dedicated sets.
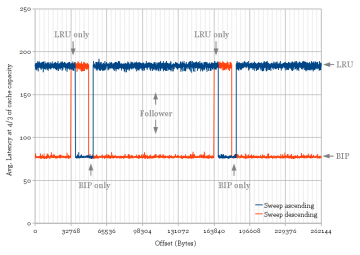
This test attempts to show set-dueling behaviour by finding which sets in the cache are dedicated and which are follower sets. This test uses a 256 KB stride (128 KB works equally well), which maps all accesses onto one set in each of the four cache slices (due to the hash function). By default, this would mean all accesses only touch the first set in each slice if the low address bits [16:0] are zero. Thus, I introduce a new parameter, offset, which adds a constant to each address so that I can map all accesses to the second, third, etc. sets in each slice instead of always the first. This parameter is swept both up and down, and the cache replacement policy used is observed.
Since the adaptive policy chooses between two different replacement policies, I chose to distinguish between the two by observing the average latency at one specific array size, 4/3 of the L3 cache size (e.g., compare Sandy Bridge vs. Ivy Bridge at 8 MB in Figure 2). A high latency indicates the use of an LRU-like replacement policy, while a lower latency indicates the use of a thrashing-friendlier BIP/MRU type policy. Figure 5 plots the results.
It appears that most of the cache sets can use both cache replacement policies, except for two 4 KB regions at 32-36 and 48-52 KB (4 KB = 64 cache sets). These two regions always use LRU and BIP/MRU policies, respectively. The plot is periodic every 128 KB because there are 2048 sets per cache slice.
The global-counter learning behaviour is seen in Figure 5 by observing the different policies used while sweeping offset ascending vs. descending. Whenever the offset causes memory accesses to land on a dedicated set, it accumulates cache misses, causing the rest of the cache to flip to using the other policy. Cache misses on follower sets do not influence the policy, so the policy does not change until offset reaches the next dedicated set.
DIP or DRRIP?
The later paper from Intel (ISCA 2010) proposes a replacement policy that is improved over DIP-SD by also being resistant to scans. DIP and DRRIP are similar in that both use set dueling to choose between two policies (SRRIP vs. BRRIP in DRRIP, LRU vs. BIP in DIP).
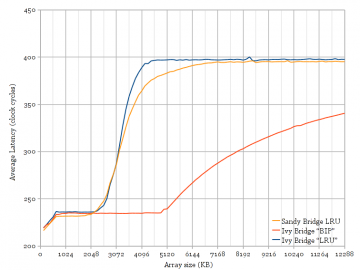
Figure 6: Scan resistance of Sandy Bridge LRU, Ivy Bridge “LRU-like”, and Ivy Bridge “BIP-like”. Pointer chasing through one huge array, and one array whose size is swept (x-axis). Replacement policy is scan-resistant if it preferentially keeps the small array in the cache rather than split 50-50. [png][pdf]
One characteristic of RRIP is that it proposes four levels of re-reference prediction. True LRU has as many levels as the associativity, while NRU (not recently used) has two levels (recently used, or not). Intel’s presentation at Hot Chips 2012 hinted at using four-level RRIP (“Quad-Age LRU” on slide 46). Thus, I would like to measure whether Ivy Bridge uses DIP or DRRIP.
Scans are short bursts of cache accesses that are not reused. SRRIP (but not LRU) attempts to be scan tolerant by predicting new cache lines to have a “long” re-reference interval and allowing recently-used existing cache lines to age slowly before being evicted, preferentially evicting the newly-loaded but not reused cache lines. This behaviour provides an opportunity to detect scan resistance by pointer-chasing through two arrays, one of which is much larger than the cache (scanning), one of which fits in the cache (working set).
Figure 6 plots the average access time for accesses that alternate between a huge array (cache miss) and a small array (possible cache hit) whose size is on the x-axis. The size of the working set that will fit in the cache in the presence of scanning is related to scan resistance. Memory accesses are serialized using lfence. Replacement policy is selected by choosing a stride and offset that coincides with a dedicated set (See Figure 5).
With half of the accesses hitting each array, an LRU replacement policy splits the cache capacity evenly between the two arrays, causing L3 misses when the small array size exceeds ~half the cache. BIP (or BRRIP) is scan-resistant and keeps most of the cache for the frequently-reused small array. The LRU/SRRIP policy in Ivy Bridge behaves very similar to Sandy Bridge and does not seem to be scan-resistant, thus it is likely not SRRIP as proposed. It could, however, be a variant on SRRIP crafted to behave like LRU.
The four-level RRIP family of replacement policies are an extension of NRU, using two bits per cache line to encode how soon each cache line should be evicted (RRPV). On eviction, one cache line with RRPV=3 (LRU position) is chosen to be evicted. If no cache lines have RRPV=3, all RRPV values are incremented until a cache line can be evicted. Whenever a cache line is accessed (cache hit), its RRPV value is set to 0 (MRU position). The various insertion policies as proposed in the paper are as follows:
- BRRIP: New cache lines are inserted with RRPV=3 with high probability, RRPV=2 otherwise.
- SRRIP: New cache lines are inserted with RRPV=2
I made some modifications for my simulations:
- BRRIP: Modified the low-probability case to insert with RRPV=0 instead of RRPV=2
- LRU-like RRIP: New cache lines are inserted with RRPV=0. This is intended to approximate LRU.
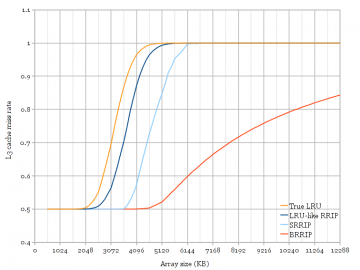
Figure 7: Cache simulations of scan resistance of several replacement policies. Ivy Bridge (Figure 6) matches very well with LRU and BRRIP policies, but does not show the scan-resistance property of SRRIP. [png][pdf]
Figure 7 shows L3-only cache simulation results of running the same access pattern through simulations of several replacement policies. The simulated cache is configured to match the Core i5 (four 1.5 MB slices, 12-way). The two policies used by Ivy Bridge (Figure 6) match very closely to LRU and BRRIP. Ivy Bridge matches less closely to a modified four-level RRIP configured to behave like LRU, and also matches slightly less well to BIP (not shown) than BRRIP. The simulation of SRRIP verifies its scan-resistance properties, which are not observed in the experimental measurement of Ivy Bridge.
I am not able to measure whether Ivy Bridge has really changed from the pseudo-LRU that was used in Sandy Bridge to a four-level RRIP. Given Intel’s hint in the slide and that Ivy Bridge behaves slightly differently from Sandy Bridge, I am inclined to believe that Ivy Bridge uses RRIP, despite the experimental measurements matching more closely to LRU than LRU-like four-level RRIP. However, it is fairly clear that Ivy Bridge lacks the scan-resistance property proposed in the ISCA 2010 paper.
Conclusion
Although the cache organization between Sandy Bridge and Ivy Bridge are essentially identical, Ivy Bridge’s L3 cache has an improved replacement policy. The policy appears to be similar to a hybrid between “Dynamic Insertion Policy — Set Duel” (DIP-SD) and “Dynamic Re-Reference Interval Prediction” (DRRIP), using four-level re-reference predictions and set dueling, but without scan resistance. For each 2048-set cache slice, 64 sets are dedicated to each of the LRU-like and BRRIP policies, with the remaining 1920 cache sets being follower sets that follow the better policy.
Code
Caution: Not well documented.
- lat.cc: Measure cyclic permutation load latency
- lat2.cc: Touch elements twice before eviction
- lat3.cc: Cycle through two arrays of different size to detect scan resistance
Acknowledgements
Many thanks to my friend Wilson for pointing me to the two ISCA papers on DIP and DRRIP.
Cite
- H. Wong, Intel Ivy Bridge Cache Replacement Policy, Jan., 2013. [Online]. Available: http://blog.stuffedcow.net/2013/01/ivb-cache-replacement/
[Bibtex]@misc{pagewalk-coherence, author={Henry Wong}, title={{Intel Ivy Bridge} Cache Replacement Policy}, month={jan}, year=2013, url={http://blog.stuffedcow.net/2013/01/ivb-cache-replacement/} }
Hi, Henry:
How did you get the data in Figure 1? I repeated the same experiments on a i7 machine, the line shows the same trend, but are much more variant than yours.
Here is the workload I use:
allocate memory size X Byte;
fill this memory (also load it into cache);
access the cache line one by one.
// Here the CACHE_LINE_SIZE is 64, and workingset_size is memsize_in_byte/CACHE_LINE_SIZE.
// The access pattern is 0, 64, 128, .. ; 1, 65, 129, ..
for (int i = 0; i < CACHE_LINE_SIZE; i++) {
for (int j= 0; j < workingset_size; j++) {
buffer[i+j*CACHE_LINE_SIZE] = 'a';
}
}
I am running it in CentOS 6.2, using Linux Kennel 3.4, I disabled speedstep, fan, and other interferences. The task is pinned to a single core. And there are no other tasks running.
Is it possible for you to explain the program a little more in detail?
Thanks very much!
Sisu
Hi Sisu,
The accesses should be data-dependent reads (with as few other interfering instructions as possible), and the access pattern should be fairly random.
The accesses should be reads: Writes are buffered so the true write latency isn’t easily observable, and you can’t make stores data-dependent on earlier stores.
Because we’re trying to measure memory latency, the load address must be data-dependent on the previous load, or the processor will attempt to issue multiple loads in parallel and hide some of the latency. In your example, the addresses are known very early (a function of i and j and not the previous load).
The access pattern needs randomness to defeat any hardware prefetching that might exist in the processor.
My code looks like this:
void** array = new void*[size]; Initialize array; void *p = (void*)&array[0]; start timer for (int i=ITS;i;i--) { p = *(void**)p; p = *(void**)p; p = *(void**)p; p = *(void**)p; p = *(void**)p; p = *(void**)p; p = *(void**)p; p = *(void**)p; p = *(void**)p; p = *(void**)p; p = *(void**)p; p = *(void**)p; p = *(void**)p; p = *(void**)p; p = *(void**)p; p = *(void**)p; } stop timerOther than loop overhead, the inner loop consists of a single load instruction that is data-dependent on the previous load. The trick is in initializing the array to contain pointers into the array itself, such that pointer chasing results in the desired access pattern. I used random cycles (variations of Sattolo’s algorithm) to defeat prefetching and allow repeatedly cycling through the array.
I should also mention that my graphs were collected using 2 MB pages (Linux hugepages) to reduce the impact of TLB misses.
Hi, Henry:
Thanks very much!
Yes, I changed my code and the lines looks much better now! *^_^*
Sisu
Did you randomize the array with similar approach?
I am a little confused about this sentence in the part of Ivy Bridge L3 Cache, “If not, the transition at 6 MB would be spread out somewhat”. My question is, if there is hash bit in [16 : 0], it means that some physical addresses will be mapped to other slice. What leads to the transition you mentioned? The latency difference between different slices? Thank you very much!
Now that I think about it, I’m less confident of that statement.
I think you’re right that it’s possible for the slice hash number to include some bits within [16:6] in the hash. As long as the cache lines are distributed evenly, this might be hard (or impossible?) to detect.
My thinking was that the set number must be exactly [16:6], even if some of those bits are used to select the cache slice. If sets aren’t distributed evenly, there tends to be some conflict misses when the cache is nearly full (leading to some cache misses with arrays slightly smaller than the cache size), but because there are some conflicts, some parts of the cache don’t get entirely kicked out due to LRU (leading to some cache hits for arrays bigger than the cache size). I’m not sure if this is entirely true, and it seems plausible that you could come up with a set number that isn’t exactly [16:6] yet still looks like a sharp transition.
One other hint that the set number is exactly [16:6] are from the larger stride accesses. Even at 128KB stride, exactly 48 cache lines fit in the L3 (corresponding to 12-way * 4 slices with all accesses hitting the same set). If the set number changed at all with 128KB-aligned addresses (i.e., if the set number includes bits [~22:17]), I would expect to see more than 48 cache lines being able to fit in the cache when using 128KB-aligned accesses.
But I could be wrong. I haven’t done any testing specifically to find out the hash function(s).
Hello Henry,
I guess, on your first chart, the fourth step represents the latency of the main memory (correct me if I am wrong). How much would that be approximately for Sandy Bridge? Does 4200 MHz represents the clock speed of a certain Sandy Bridge processor ?
Thank you for your time.
Yes, the last step is main memory (and some TLB miss latency in there too). As you can see from the graph, it’s about 230 cycles with a L1 TLB hit on my system (at 4.2 GHz, with my particular DRAM timings).
4.2 GHz is the speed at which I’m running my processor (overclocked Core i5-2500K).
Hi Henry,
Great discussion. I am a hardware guy and OK C programmer, but have little experience with C++. I tried to compile lat.cc, lat2.cc, and lat3.cc on a MacPro using clang based on LLVM 3.5 and received the following warnings and errors. Any suggestions on where I need to start looking on fixing this? Thank you for any help!
Charless-Mac-Pro-2:cache_test charles$ clang lat.cc
lat.cc:163:34: warning: data argument not used by format string [-Wformat-extra-args]
printf (“%f\n”, clocks_per_it, dummy); //passing dummy to prevent optimization
~~~~~~ ^
lat.cc:165:60: warning: data argument not used by format string [-Wformat-extra-args]
printf (“%lld\t%f\n”, size*sizeof(void*), clocks_per_it, dummy); //passing dummy to prevent optimization
~~~~~~~~~~~~ ^
lat.cc:241:59: warning: data argument not used by format string [-Wformat-extra-args]
printf (“%lld\t%f\n”, size*sizeof(void*), clocks_per_it, dummy); //passing dummy to prevent optimization
~~~~~~~~~~~~ ^
3 warnings generated.
Undefined symbols for architecture x86_64:
“operator delete[](void*)”, referenced from:
_main in lat-b1c906.o
“operator new[](unsigned long)”, referenced from:
_main in lat-b1c906.o
ld: symbol(s) not found for architecture x86_64
clang: error: linker command failed with exit code 1 (use -v to see invocation)
Charless-Mac-Pro-2:cache_test charles$ clang –version
Apple LLVM version 6.0 (clang-600.0.56) (based on LLVM 3.5svn)
Target: x86_64-apple-darwin13.4.0
Thread model: posix
The three warnings are expected. I’m deliberately passing in an argument to printf that isn’t used, just to avoid compiler optimization (It’s in the comment for that line).
The errors don’t make much sense to me. I wonder if it’s because you need to compile with clang++ (a C++ compiler) rather than clang (a C compiler)? Allocating and freeing arrays using new and delete is straightforward code, so I wouldn’t expect compilers to complain about them.
DUH!!
I had it in my mind that clang detected the different file types by suffix name and processed accordingly; such as what It does with .h, .s, .o, .c files.
Thank you for the fast response. (I’m glad my last name is not on here; how embarrassing!)
I didn’t get the sharp bends shown on your charts, but got the data I wanted. Thanks again for an excellent article.
gcc vs. g++ also gives out some strange linker errors if you compile C++ with gcc.
The sharp bends are because the memory access pattern uses a cacheline stride (i.e., use -cyclelen 8 because 8 64-bit pointers fit in a 64-byte cacheline), and also from reducing TLB misses by using 2MB page size. Using 2M pages is rather OS-specific though, so I doubt that would work on OSX without some changes.
Hi,
Thanks for the post I found it very interesting. Is there any chance you could post the compiler flags and test flags that you used for each graph as I am struggling to reproduce some of the graphs.
Many thanks
Daniel
I just used -O2. The compiler flags have little effect. As long as variables are put into registers, there’s not much other optimization the compiler can do.
Do note that these graphs were run using 2MB pages. Also, having transparent hugepages enabled will affect the graphs (because some pages are 2M but others not).
Thanks for posting this information!
You raised the question of what hash function Sandy/Ivy Bridge CPUs use to map physical addresses to cache slices.
That is answered by the 2013 paper “Practical Timing Side Channel Attacks Against Kernel Space ASLR” (which covers 4-core CPUs) and my recent blog post “L3 cache mapping on Sandy Bridge CPUs” (which covers 2-core CPUs too).
Cheers,
Mark
For this testing, do you know what RAM memory you were using?
Specifically, what size were the DIMMs and were they single or dual rank?
Hmm… at the time, I think it was 2 * 4GB DDR3 DIMMs. dmidecode is telling me Rank=2. It was probably F3-14900CL9-4GBXL in both systems.
How much does it matter (would it show up in the measurements)?
Not sure.
If possible, I’d like to run the code you used to produce data from “Choosing a policy using set dueling” section.
Would you be able to share this?
The code is already posted (It’s at the bottom of the article in section “Code”). If I remember correctly it’s lat3.cc.
Hm, actually, it looks like it’s lat.cc, using -offsetmode (with -startoffset and -stopoffset)
Thank you for clarifying, wasn’t sure which code applied
Great article! I’m experiment with your code and wandering how can I change the parameter “stride” in it? I can’t produce the sharp raise of latency.
OK, cyclelen. I get it. A bit of confusing, but I get it 🙂
Haha, sorry. The code evolved over many years (for various things) and I didn’t really spend much effort cleaning it up before posting it…
Hi Henry, it’s a much later time now so I don’t know if you will get this but if you do, how can I simulate cache accesses. I mean, trying to access data in L1, L2, LLC and measuring the latency.
Hello!
What do you mean by “simulate”? To me, that means writing a simulation model of how I think the cache hierarchy should behave, and then seeing how various access patterns behave. That’s the opposite of actually measuring the actual latency on real hardware, which is what your second sentence sounds like.
The simplest simulation model (which is roughly what I did here) is to have an array containing the state of each cache line, then for each cache access, recording whether it was a hit or miss, and updating the cache line state (according to the replacement policy).
Hardware measurement is a bit harder. You need to construct an access pattern that you know will ~100% hit in one particular level of the cache hierarchy, and ensure there is no parallelism between different memory accesses, then measure the runtime of some number of them. I like to use random cyclic permutation pointer chasing that touches each cache line in an array exactly once before repeating the sequence. This access pattern satisfies most of the requirements at the same time (no parallelism between accesses, relatively easy to control which level of cache to hit, defeats hardware prefetchers, low overhead per access).
Hey Henry, great article! Thank you for sharing!
Can I have some reference for the dual pointer chase, how and why does it work for adaptive policies? A small example could help maybe.
I don’t think there’s a reference for the “dual pointer chase”. I just made it up and used it.
I wouldn’t say it works for “adaptive policies” in general. It’s designed to work specifically for policies that try to detect access patterns where you touch the data exactly once and then evict it from the cache without reuse (“scanning” behaviour). To test whether there is a replacement policy that tries to detect access patterns where there is no reuse, I will create a very similar access pattern where there is reuse before eviction, and see if it behaves differently than if there were no reuse.
The basic cyclic access pattern is something like:
ABCDEFGHIJKL........ABCDEFG...(A, B, C, etc. are not consecutive, they’re random cache lines)The dual pointer chase is something like:
A_B_C_D_E_FAGBHCIDJEKFLGMHNIOJPKQLRMSNTO...It touches the same sequence of cache lines a second time, but somewhat delayed. The intent is so the cache thinks every line has been touched twice before being evicted.
Hi Henry,
I currently do research regarding eviction policies.
why did you write the loop like that?
for (int i=ITS;i;i–)
{
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
j = *(void**)j;
k = *(void**)k;
}
and not like that:? (with the appropriate iteration you need)
for (int i=ITS;i;i–)
{
j = *(void**)j;
k = *(void**)k;
}
I will be happy to talk with you by email, I am sure that you can contribute a lot of information to me 🙂
Thanks, Tom